|
|
|
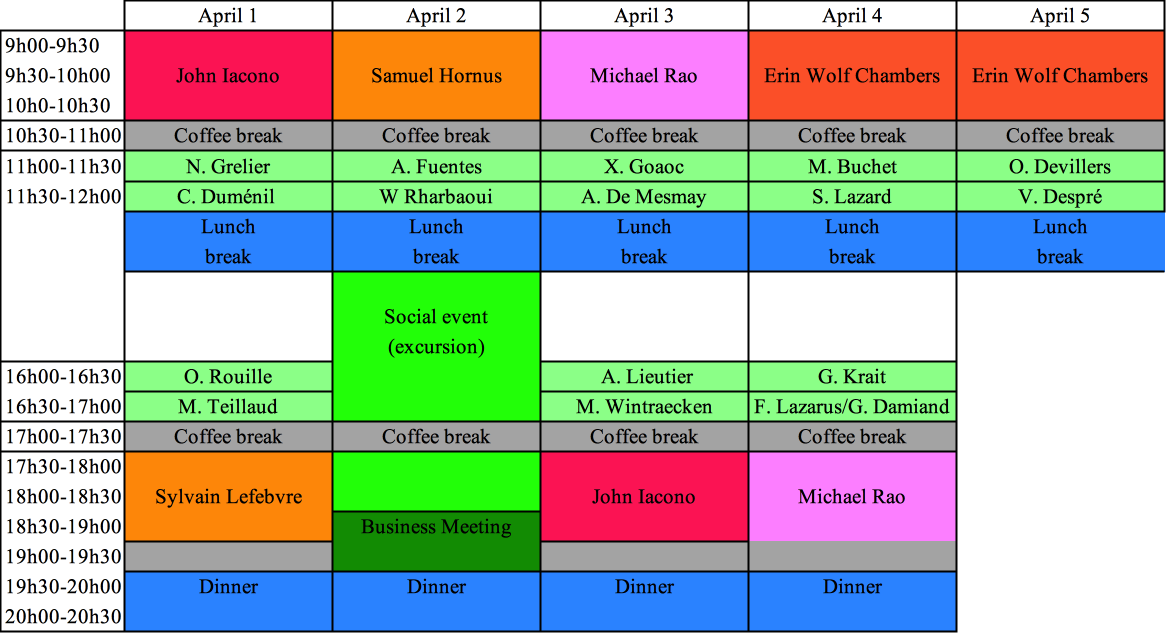
Program
LECTURES
In the first part we will look at how several non-geometric data structures can be transformed into an equivalent geometric view, which results in being able to apply geometric results and intuition to seemingly non-geometric problems. In the second part we will look at ideas of optimality of geometric problems. What really does it mean for an algorithm to be optimal? We will examine worst-case, output sensitive and instance-optimality through the lens of some classic geometric problems. In both parts several outstanding open problems and avenues for future research will be presented.
Part 1: The four color theorem. The computer is more and more used to prove theorems in mathematics. I will introduce the subject with the famous "four color theorem", its history and his proofs. It's the first important theorem proved with the help of a computer, and is a good example to show the advantages and the questions of this kind of approaches. Part 2: Exhaustive search of all convex pentagons which tile the plane. In 1918, Karl Reinhardt asked which convex polygon can tile the plane, and the pentagons was the only opened case. Fifteen types of such pentagons have been found between 1918 and 2015. I present an exhaustive search of all families of convex pentagons which tile the plane. This proof is in two parts. First we show that if a pentagon tiles the plane, then it is in one of 371 families. Then a computer program tries, for each family, all possible tile arrangements, and shows that there are no more than the already known fifteen types. In particular, this implies that there is no convex polygon which allows only non-periodic tilings.
Fused filament fabrication (FFF) 3d-printers are very cheap and very popular.
The question of how to measure similarity between curves or 3d objects in various settings has received much attention recently, motivated by applications in GIS data analysis, medical imaging, and computer graphics. Geometric measures such as Hausdorff and Fr\'echet distance have efficient algorithms, but often are not desirable since they do force any deformation based on them to move continuously in the ambient space. In this talk, we'll consider measures that instead are based on the usual of topological maps between objects, such as homotopy or homology. Such deformations will generally look to minimize some quantity of the map between the two objects, such as total area swept or longest intermediate curve. We will survey several measures (both geometric and topological) which have been introduced and studied in recent years, with a focus on curves in various settings but also with some discussion of 3d objects in Euclidean space. The talk with address structural properties of these maps, as well as considering the complexity of the problem or known algorithms to compute them. We will also give an overview of the many remaining open questions connected to these measures. _________ Book of abstracts of short talks: Book Slides of short presentations: Computing hyperbolic structures from Thurston's equations. Owen Rouille, Clément Maria Poisson sample and 3D-Delaunay on surface. Charles Duménil, Olivier Devillers An implementation of the homotopy test in CGAL. Expected Complexity of Routing in Theta-6 and Half-Theta-6 Graphs. Olivier Devillers Hard problems in knot theory. Arnaud de Mesmay, Yo'av Rieck, Eric Sedgwick, Martin Tancer
|